链表如果有环,找到环的起点
问题
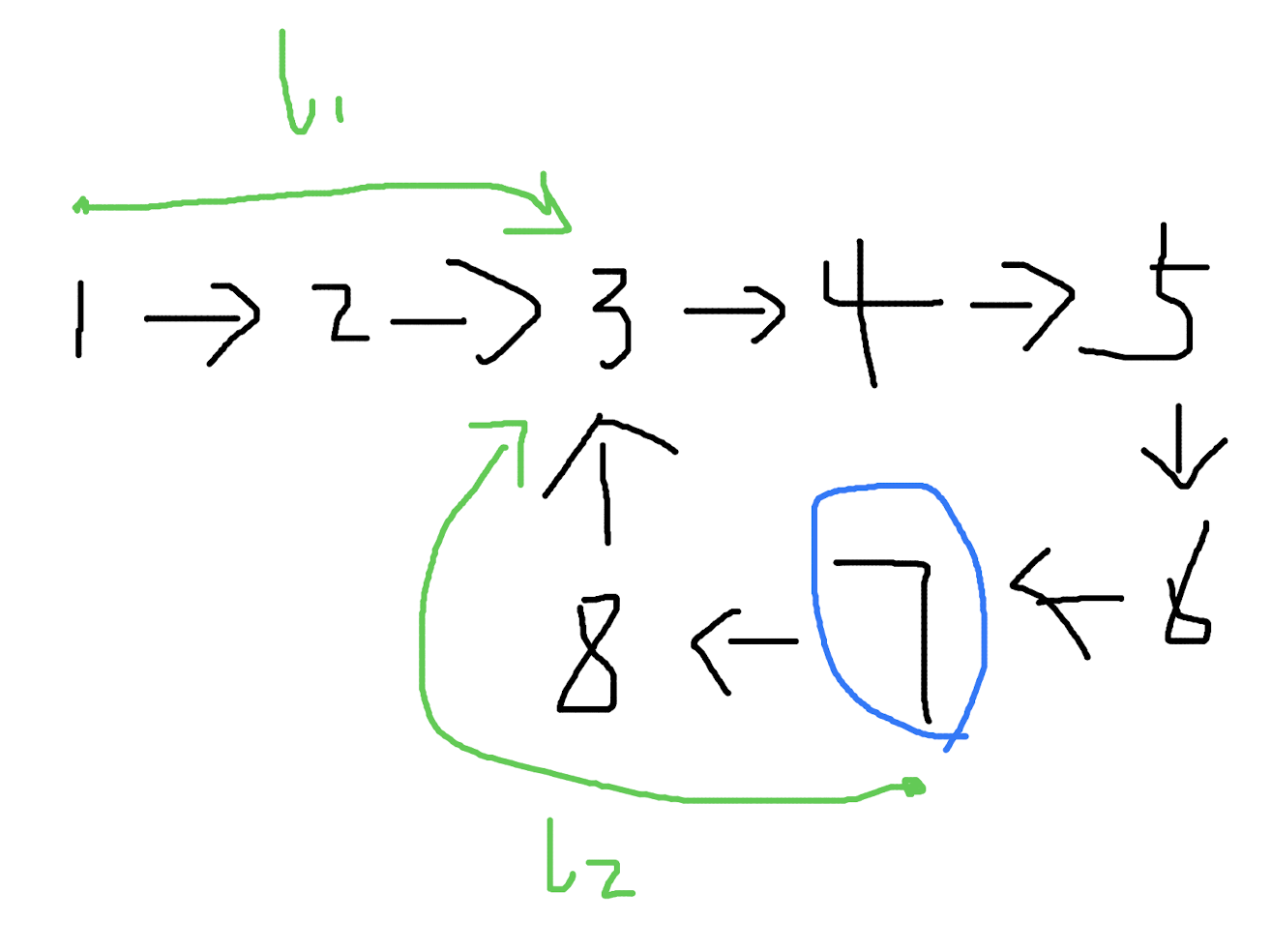
这个问题是上一个问题的延伸,在判断链表已经有环的基础上,找到环的起点。比如这样的一个链表,环的起点是节点 3。
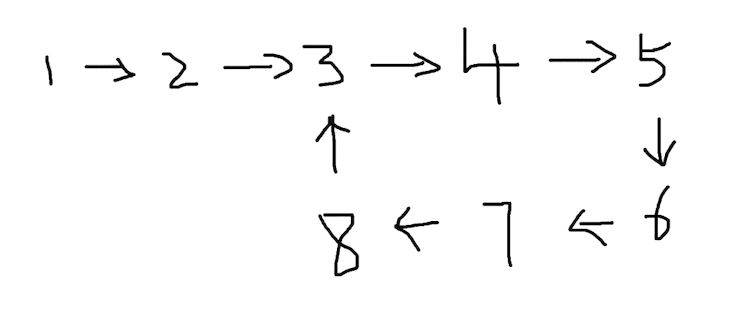
分析
(1)
在判断链表是否有环的问题中,我们得到了一个至关重要的结论:
t = R
两个快慢指针将会在等于环长度的时间点相遇。对于上图的链表,快慢指针的位置关系是这样:
| 时间 t | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| A 的位置 | 节点 1 | 节点 2 | 节点 3 | 节点 4 | 节点 5 | 节点 6 | 节点 7 |
| B 的位置 | 节点 1 | 节点 3 | 节点 5 | 节点 7 | 节点 3 | 节点 5 | 节点 7 |
我们可以观察到,环的长度是 6,快慢指针也会在第 6 秒相遇,他们交点位置是节点 7:
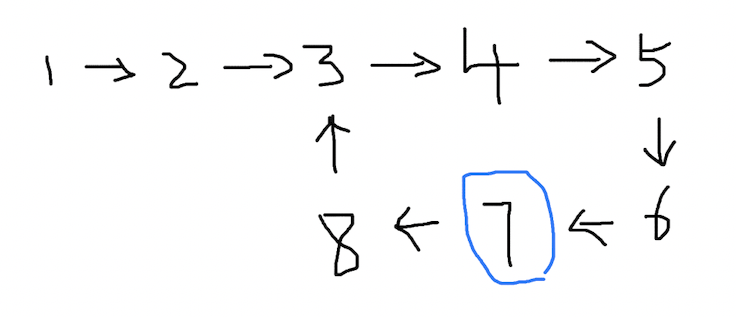
(2)
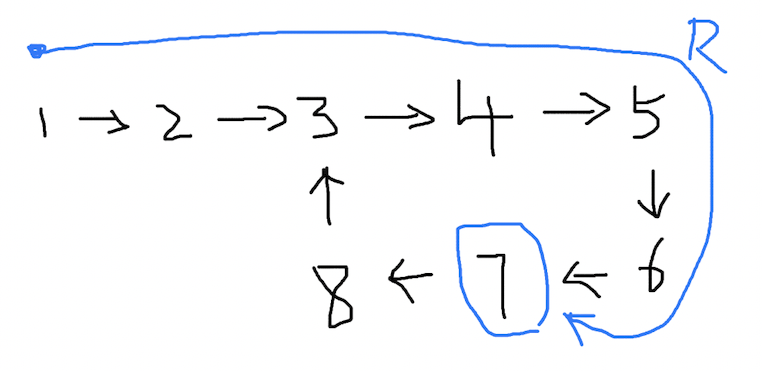
根据上面提到的之前的结论,按照慢指针 v1 = 1 的速度,它经过的路程和时间是一样的,也就是说,从出发点到两指针相遇的路径长度,根据 t = R,此刻的时间是 t,正好是环的长度 R:
(3)
做一个假设,慢指针保持着这个长度为 R 的走过的路径,向前移动一步,会变成这样:
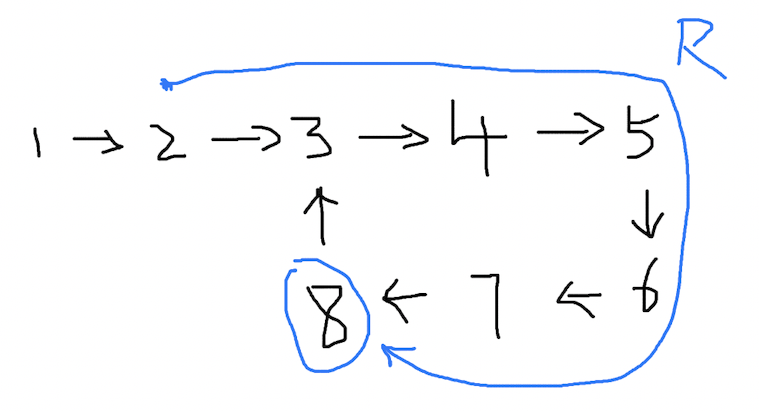
再走一步,变成了这样:
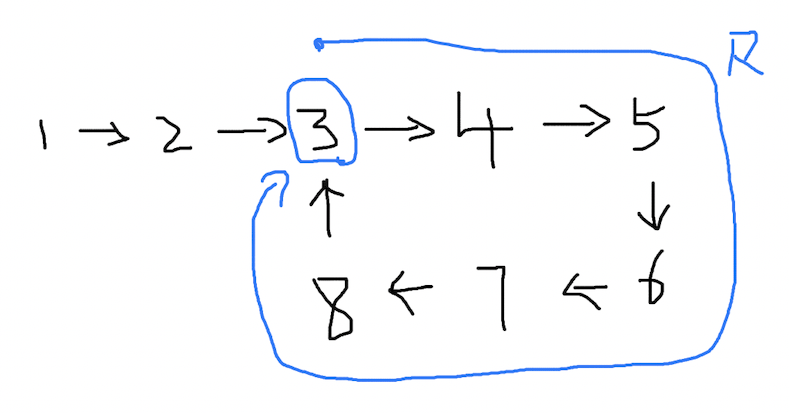
(4)
到这里似乎还不知道我们要干什么。现在对路径设一个变量,从 出发点 到 环的起点 之间的距离设为 l1,整个链表的长度设为 l,环的长度仍然为 R。
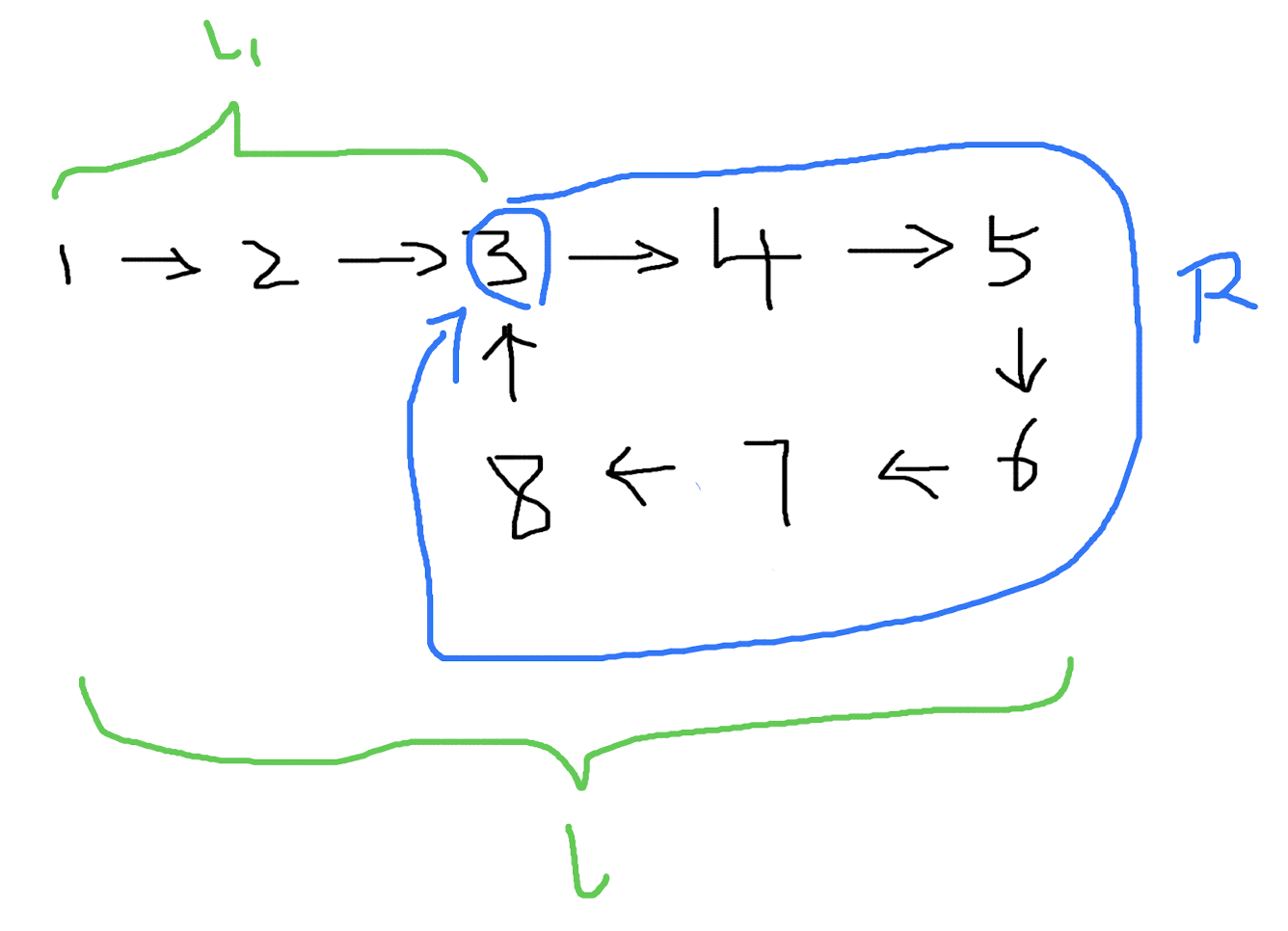
这 3 个变量将满足这样的关系:
l - l1 = R
这是太显而易见的事情。
(5)
记得我们一开始的结论吗?从 出发点 到 快慢指针的交点 之间的距离,等于环的长度 R:

变量 l 和 l1 保持不变,图就成了这样:
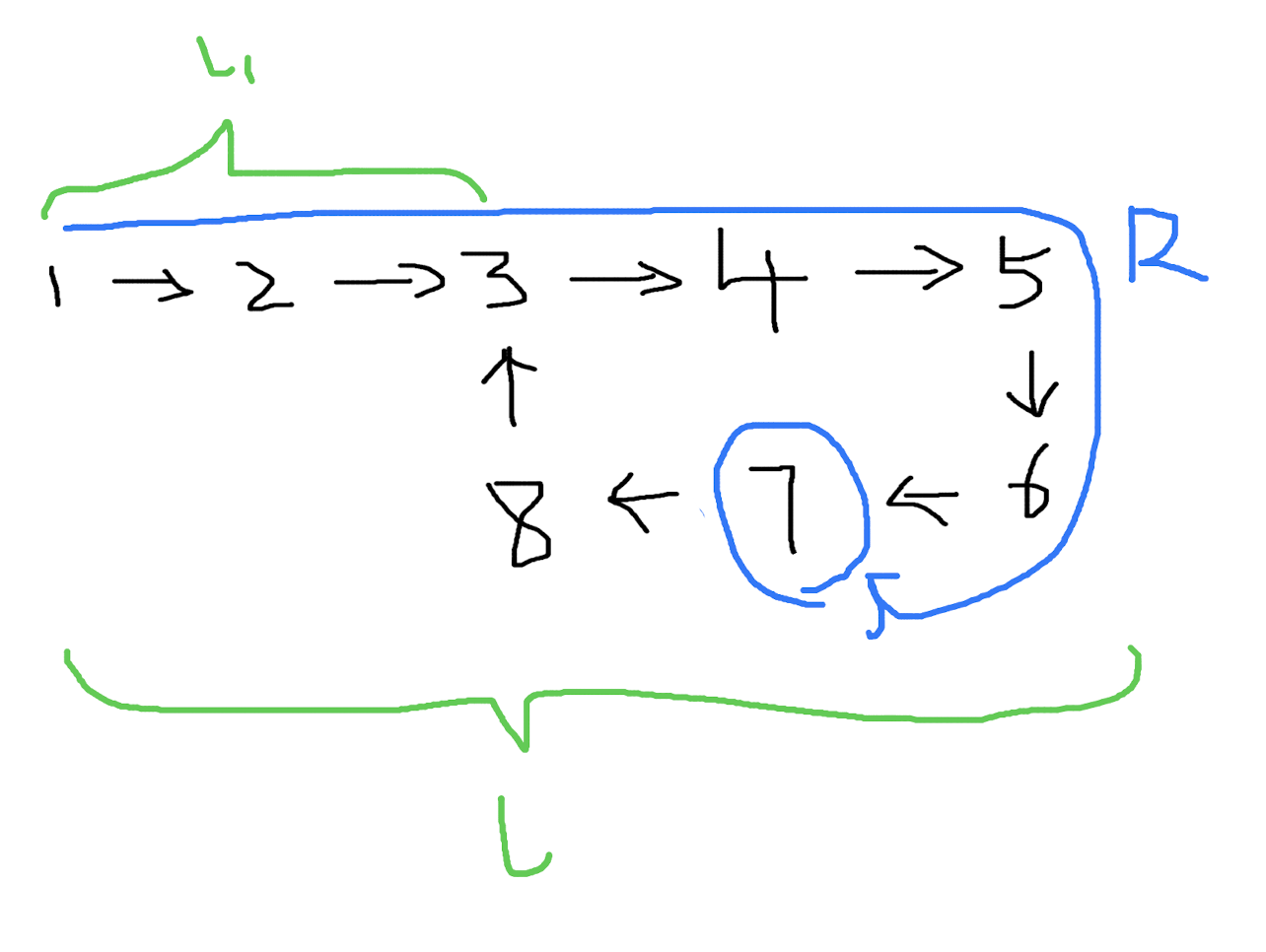
此时的 l 仍然等于 l1 + R,不同的是,l1 和 R 重合了。
(6)
l - l1 = R
重合之后,等式关系还成立吗?当然成立,因为整个链表没有变,变量的大小没有变。但好像又觉得哪里奇怪。
现在新设一个变量,设从 快慢指针的交点 到 环的起点 的距离为 l2:
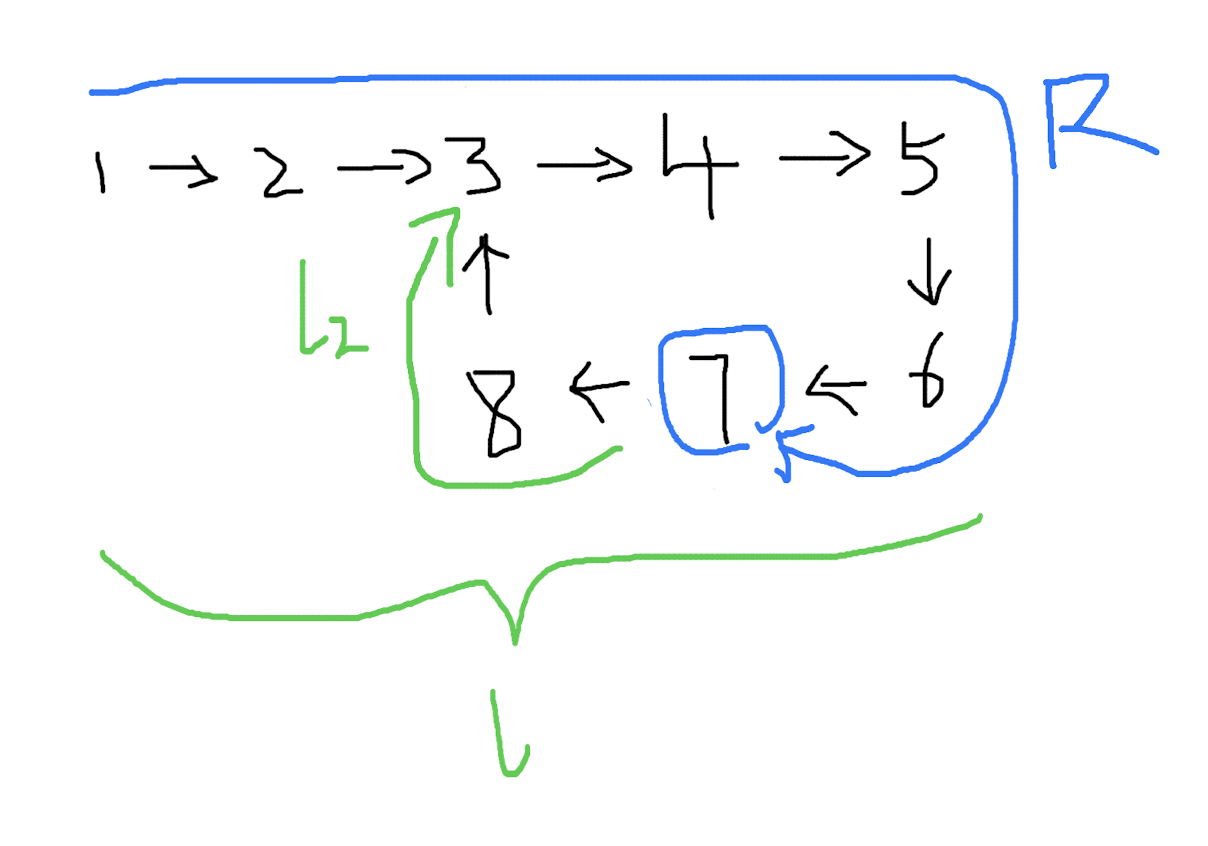
此时:
l - l2 = R
(7)
经过这样一些比较,发现 l1 == l2,也就是从 出发点 到 环的起点 的距离,等于 快慢指针的交点 到 环的起点 的距离。
解决
出发点 -> 环的起点 == 快慢指针的交点 -> 环的起点
这是一个很重要的结论,因为我们此时的快慢指针就在 快慢指针的交点 上,在节点 7 的位置。
如果这个时候在新增一个指针 p3,在快慢指针相交的时刻,从整个链表的 出发点 1 出发(速度为 1),那么 p3 和慢指针一定会相交,因为 p3 到 环的起点 的距离等于慢指针到 环的起点 的距离。p3 遇到慢指针的位置,就是环的起点。